 有趣的二进制
有趣的二进制
在计算机中数据的存储都是以0与1表示的,存储设备上也仅有这2种状态,即称为二进制;在开发过程中,高级编程语言直接使用二进制的情况很少,因为底层已经做了很多封装,但是实际开发过程中了,为提高数据运算效率,二进制运算是一个不错的选择。
在实际工作中,有数据参与计算,使用二进制能够显著的提高代码运行效率,接下来主要介绍二进制运算、以及归纳常见的进制运算技巧。

# 1. 正负数的存在形式
通常在数运算过程中使用 + 和 - 来表示正负数,但是计算机中都是以 0 和 1 二进制表示,那么怎么表示负数呢?于是就有了符号位的存在,在二进制中使用 1 来表示符号位,负数是以绝对值二进制的反码存在的,负数的二进制可以通过绝对值的二进制转换而来(正数),转换过程就有原码、反码、补码的存在。
- 原码:若字长为n,那么一个数的原码就是用一个n位的二进制数,最高位为符号位:正数为0,负数为1;剩下的n-1位为数的绝对值,位数不够的用0补全。
- 反码:在原码的基础上,最高位符号位不变,其他位取反(0变1,1变0),也就是n-1位取反得到;
- 补码:在反码的基础上,根据二进制做加1运算(逢2进1);
注意: 正数的原码、反码、补码都是一样的
如下以1个字节8位二进制说明正负之间的关系。
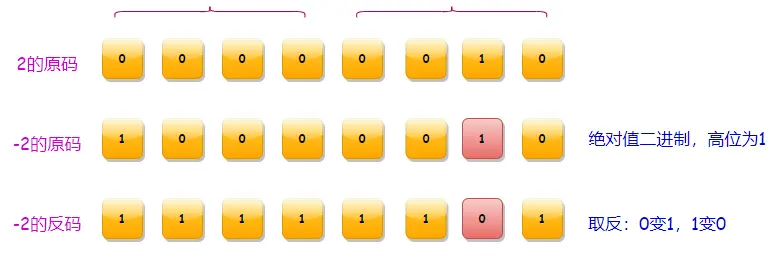
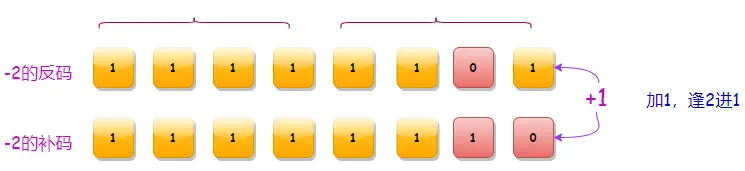
无论是8位还是16位、32位计算方式都是一样的。
# 2. 二进制的运算
# 2.1. 与运算&
两个位都为1时,结果才为1,通常
与运算,用于取值
88 0101 1000
66 0100 0010
& ———————————
64 0100 0000
2
3
4
# 2.2. 或运算|
两个位都为0时,结果才为0,通常
或运算,用于填值
88 0101 1000
66 0100 0010
| ———————————
90 0101 1010
2
3
4
# 2.3. 异或运算^
两个位相同为0,相异为1
88 0101 1000
66 0100 0010
^ —————————
26 0001 1010
2
3
4
# 2.4. 取反运算~
进制取反,0变1,1变0
88 0101 1000
~ ———————————
-89 1010 0111
2
3
# 2.5. 左移运算<<
二进位全部左移若干位,高位丢弃,低位补0
66 0100 0010
1 << ——————————
-124 1000 0100
2
3
# 2.6. 右移运算>>
二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移)
66 0100 0010
>> 1 —————————
33 0010 0001
2
3
# 2.7. 无符号右移运算>>>
二进位全部右移若干位,无论是否存在符号位,都补0
66 0100 0010
>>> 1 —————————
33 0010 0001
#8位无符号右移,符号位参与位移,高位补0,也就去掉符号,变为正数了
-2 >>> 1 = 127
1111 1110
>>> —————————
127 0111 1111
2
3
4
5
6
7
8
9
10
# 3. 常见的运行技巧
在实际工作中,若经常阅读源码,也就经常遇到需要奇怪的魔法值或者位运算,出现必定合理,一定是有理论原来支撑和提高效率的运算技巧,下面汇总一些场景的技巧。
# 3.1. HashMap中的运用
在HashMap中基于高低位异或来计算KEY存在数组下标位置,这里与扰动函数有关,可自行搜索相关原理,其主要是为了让数据分配更合理,避免碰撞。
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
2
3
4
在 HashMap 中,为了提高计算效率,在元素存储容量上也很有讲究,HashMap中Size 必须是2的倍数,也就是2的幂次方,如下则通过位运算来判断是否是2的幂等次。
一开始看可能不知所措,其实是有原因的,int 正数用32位bit位表示的,通过移动对应位数,通过或运算来设置对应位上的值。

如源码,cap-1移动分别移动1、2、4、8、16位并做或运算,其实为了给各个位置填1,设置位1后得到的数也就是2的幂等次减1的数,最后位移结果加1即可。
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
2
3
4
5
6
7
8
9
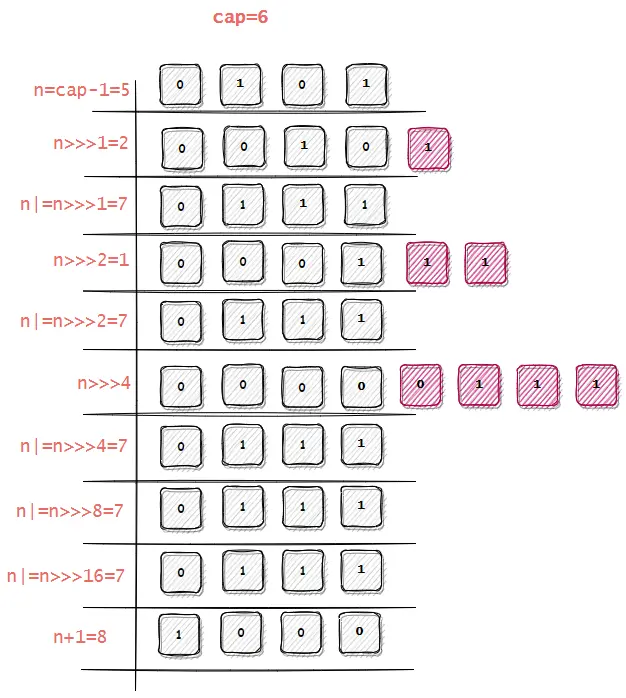
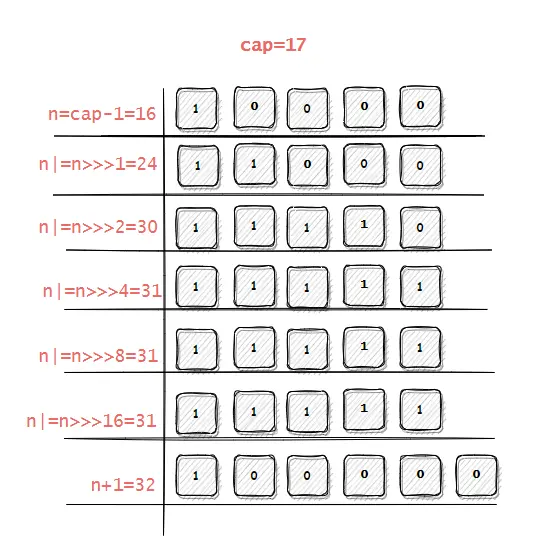
在特殊情况下,可以用位运算符 & 来取代 %,从而提高程序运行效率。当两个整数a % b , 恰好b等于2的N次方的时候(如2、4、8、16……),可以使用a & (b-1)计算,比如: 9 % 4 = 9 & 3,其实无论 a 替换为什么数,都可以满足,也就可以快速求余计算。
对于证明一个数是否是2的幂可通过2种与运算验证:n & (n - 1)=0 或 n & (-n) = n
# 3.2. 求奇偶数
通常判断一个数的奇偶性通过与2整除,取余来判断,还可以采用位运算来判断,非常高效,如n&1=0为偶数,n&1=1为奇数,其本质就是判断二进制位中最后一位,为1(n & 1 = 1)则为奇数,为0(n & 1 = 0)则是偶数。
# 3.3. 两个数的交换
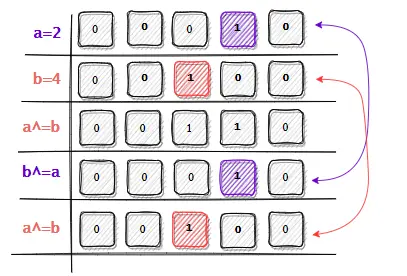
通过位运算巧妙地实现两个数无需变量交换,如图通过 a^b 计算得到承载2个数的数 00100,最后分别与 a、b进行异或就能得到交换后的数。
# 3.4. 其他技巧
| 功能 | 示例 | 位运算 |
|---|---|---|
| 乘以2的运算 | (0100->1000) | n << 1 |
| 除以2的运算 | (0100->0010) | n >> 1 |
| 乘以2的m次方 | n*(2^m) | n << m |
| 除以2的m次方 | n/(2^m) | n >> m |
| 去掉最后一位 | (101101->10110) | x >> 1 |
| 在最后加一个0 | (101101->1011010) | x << 1 |
| 在最后加一个1 | (101101->1011011) | x << 1+1 |
| 把最后一位变成1 | (101100->101101) | x | 1 |
| 把最后一位变成0 | (101101->101100) | x | 1-1 |
| 最后一位取反 | (101101->101100) | x ^ 1 |
| 把右数第k位变成1 | (101001->101101,k=3) | x | (1 << (k-1)) |
| 把右数第k位变成0 | (101101->101001,k=3) | x & ~ (1 << (k-1)) |
| 右数第k位取反 | (101001->101101,k=3) | x ^ (1 << (k-1)) |
| 取末三位 | (1101101->101) | x & 7 |
| 取末k位 | (1101101->1101,k=5) | x & (1 << k-1) |
| 取右数第k位 | (1101101->1,k=4) | x >> (k-1) & 1 |
| 把末k位变成1 | (101001->101111,k=4) | x | (1 << k-1) |
| 末k位取反 | (101001->100110,k=4) | x ^ (1 << k-1) |
| 把右边连续的1变成0 | (100101111->100100000) | x & (x+1) |
| 把右起第一个0变成1 | (100101111->100111111) | x | (x+1) |
| 把右边连续的0变成1 | (11011000->11011111) | x | (x-1) |
| 取右边连续的1 | (100101111->1111) | (x ^ (x+1)) >> 1 |
| 去掉右起第一个1的左边 | (100101000->1000) | x & (x ^ (x-1)) |
# 4. 总结
通常对于位运算的使用过程中,是最直接,参与底层交互计算的,能够提高计算效率;同时每一种参与二进制运算的背后都有数学计算理论支撑的。
| 符号 | 含义 | 规则 | 备注 |
|---|---|---|---|
& | 与 | 同1则1 | |
| | 或 | 同0则0 | |
~ | 非 | 0变1,1变0 | |
^ | 异或 | 相同则0,相异则1 | |
<< | 左移 | 高位丢弃,低位补0 | |
>> | 右移 | 高位补0,低位丢弃 | 有符号,符号位不变 |
>>> | 无符号右移 | 高位补0,低位丢弃 | 符号位一起移动 |
